信号のデジタル化には、サンプリングに際して必然的に発生してしまう不要な高い周波数を如何にして取り除くかという問題が、どれだけの量子化ビットが必要かという話も含めて常に付きまとう。音声の分野で最初に始まったのは、概念としては理解しやすいPCM方式。これはあまりサンプリング周波数は考えない。標本化定理の少し上ぐらいなら良かろう、程度で終り。CDの44.1kHzのように。
替りに、量子化ビットには拘った。16ビットは当時の技術水準からすると、過剰品質。ADCは勿論、DACも家庭用として価格的に実用的なものはなかった。PCM の性として、そっちに拘ってしまう傾向があるので、そこまで頑張ったんだと思う。現実のアナログ素子としては、今も16ビットはほぼ限界。単調増加を保証しているマルチビットの16ビットDACは、そんなに多くない。
そんなPCMの原理的宿命を回避するのがDelta_Sigma_Modulation、所謂DSM。DSMはあまり大きなビット数を必要とせず、おそらく製造上のプロセスの関係からデジタルフィルターなどのデジタル素子との親和性も高いので、アナログプロセスの必要なマルチビットと比べて、安く高性能にできる。問題は、些かその理論的背景が複雑なので、PCM程には直感的理解が難しい事になっている。
それは元々DSMが、1ビットで出来ているデルタ変調に源があって、多くの場合は1ビットで語られることが大きな要因。更には、どうして1ビットでまともな音が出るのかという、DSMの根源的な問いに対して直観的で明確な答がないという事。PCMのどうしてナイキスト周波数はたったの2倍で良いのか、よりもハードルは高い。
PCMですら、デジタルのギザギザでアナログの音は出ないと未だに拒否感があるので、更にDSMの1ビットと来るならば、黒船扱いされるのも致し方なし。とはいえ、今はDSM以外のDACはとても稀なマニア向けになってしまっているのも事実。DSMが難しいかというならば、必ずしもそうではない。直感的に理解していると思っているPCMの方が、実は複雑と言っても嘘でない。
それは、初めに1ビットなし。DSMの歴史は1ビットに始まっているけれど、原理的にはそうではないので。1ビットを止めてしまうと少し話は分かり易くなる。1ビットもあるけれど、今のDSMDACは6ビットぐらいが多い。解析する時も、その位が宜しい。これは単に量子化器の問題なので、ビット数はあまり関係がない。必ず出てくるノイズシェービングという一種の積分器の数は、3か5か7かで大きく変わってしまうのだけれど。
下の図は大抵の教科書に出て来る、基本的な一次のDSM。但し問題なのは、ほとんどの場合は触れられてないけれど、この図は4通り存在する。入力と出力がアナログなのかデジタルなのか。アナログ(入力)-デジタル(出力)、デジタル(入力)-デジタル(出力)という按配で4種類が存在する。前者はDSMのADCで、後者はPCMからDSMへの変調器で、良く使われるのはこの2つ。この図は後者のDSM変調器で、ここではこれ以外は扱わない。ほとんど全ての教科書は、この4つを断りなく混在させるので、読む方は全く分からなくなる。おそらく、書いている人だって分かってない。分かっているならば、必ず断りを入れる。そうでないと、本人でも分からなくなる。

この図をとっつきにくくしているのは、Z^(-1)というやつ。俗にz変換と言われるが、これは単純に1クロック分の遅延。74HC374というICと同じもの。デジタルの話なので(ここでは全てのデータがデシタルの場合しか扱わない)、v(n)の一つ前のデータはv(n-1)で、v(n-1)=z^(-1)*v(n)が成り立つ。なので、z^(-1)がなくてもこの回路図の入力と出力の関係は数式化できる。
出力のv(n)を1クロック遅らせたものを入力のu(n)から引いて(u(n)-v(n-1))、これに量子化器の入力であるy(n)の1クロック遅延を足したのがy(n)。
つまり、 y(n)=u(n)-v(n-1)+y(n-1)
知りたいのは入力のu(n)と出力のv(n)の関係なので、量子化器の入力のy(n)は些か邪魔だけど、量子化器という線形でないものを含むので多分これは仕方ない。
この数式が全てのDSMの基本であるけれど、これが何を意味するのかは全く分からない。元々DSMも、デルタ変調に積分器を入れてみたら上手く行った、という偶然の要素から生まれているのので、これは結果オーライしてしまった。
そこで少しばかり発想を変える。このようにして出力を入力に戻すと、これはOPアンプのNFBのように機能する。量子化器のために出力は入力と同じになる事はない。つまり必ず歪は存在する。しかしNFBなので、量子化器で決まるある一定値を超えて出力が入力に外れる事はない。なので誤差つまりは歪は、そんなに大きくならないのではと期待できる。ならばと、デジタルの単純なNFBを考える。こんな具合。

量子化器の入力y(n)と出力v(n)の差であるy(n)-v(n)を1クロック遅延させてから入力のu(n)に足し、これを量子化器の入力y(n)とする。量子化器で発生する誤差を入力にNFBするだけ。これは1クロックの遅延がミソ。この遅延がないと、デジタルの回路はNFBであっても発振してしまう。エクセルでは、巡回参照のエラーとなる。
この場合のy(n)は、
y(n)=u(n)+y(n-1)-v(n-1)となる。これは前述の
y(n)=u(n)-v(n-1)+y(n-1)と同じ結果。つまり、デルタ変調から発生したDSMの基本回路とは、単純なデジタルのNFB以外の何物でもない。一次のDSMとは、量子化器で発生する誤差を入力にNFBさせているだけの事。
この2つの図は機能的には同じ。最初のは積分器というのが入っているので、さてこれは何だろうかと引っかかる。積分器なので、入力が直流であるとかならず飽和する。積分器とは足し算なのだから。なので符号を変えて足している。所謂NFB。2つ目はならばとNFBを考えただけで、積分器だとかDSMだとかノイズシェービングとかは一切考えていない。必要もない。
この数式は、z変換とも無縁な単なる漸化式なのでシミュレーションは容易。エクセルで簡単にできる。今はmatlabとかpythonが主流で、エクセルはお子様ランチみたいな感なきにしもあらず。でも漸化式を視覚的に一つ一つ追いかけるのであれば、表計算に勝るものなし。こんな具合に視覚化できるのが一番良い。

これは5ビットの量子化器を使っている。どうもハードウエア化する場合、6よりも5のほうが上手く行くので。カラムのEが量子化器の出力。入力を16ビットで6kHzにして48kHzでサンプリング。64倍のオーバーサンプリングで計算。どうしてオーバーサンプリングかという問いは、誤差であるカラムFをグラフ化すると、感覚的に理解できる。

青が量子化器の出力v(n)。ほとんど重なって見えないけれど、緑が入力のu(n)。赤が量子化器での誤差であるy(n)-v(n)。もしも青が緑と同じであれば、赤はゼロで誤差がないという事。赤のFFTをとればこのNFB回路、つまりは一次のDSM変調器の歪が分かる。赤を、カラムFを小さくすれば、この5ビットDSMの歪は減るという話。
縦軸の電圧方向は単純。量子化器のビット数を上げれば小さくなる。今は5ビットなので1/32ぐらいの最大値となっている。但し、問題は音声帯域内での歪なので、あまり電圧方向は効果がない。このコサイン波形は6kHzなので、赤の時間軸方向の解像度はかなり高い。解像度の高さは高い周波数成分を意味するので、全体のレベルは高くても音声帯域での歪成分は小さい筈。つまりは、音声帯域では低く帯域外では上がる、所謂ノイズシェービングが自動的にかかっている。
さらに2倍して128倍にしたならば、更に高い周波数成分を意味するので音声帯域の歪は減る。電圧方向(量子化ビット)よりも、周波数方向の対策(オーバーサンプリング)が有効だという事を赤は言っている。実際のFFT結果はこう。

こんな単純なデジタルNFBでも-66dB(0.05%)ぐらいの歪。16ビットのPCMの場合も、同じように入力と出力と誤差をグラフ化するとこう。

言うまでもなく、赤のPCMでの誤差はかなり大きい。電圧方向は16ビットあるのでほぼ無視できるけれど、時間軸での歪が大きいので。8点しかサンプリングできないので当然と言えば当然。DSMでの赤とはかなり違う。但し誤差のスペクトル(対域外に無限に出るイメージ)は、サンプリング周波数の整数倍の両脇に大きなピークが出来るので、デジタルフィルターやアナログフィルターで取り易い。
FFTから分かるように、ナイキスト間隔内では圧倒的にPCMが有利。16ビットの理論値とほぼ同じで0.001%ほど。しかし42kHzと54kHzには、10%を超える歪が出る。更に上の所にも無限に出る。いくら電圧方向に拘っても、PCMには限界がある。これは標本化定理の要求する理想フィルターとも通じる。時間軸方向を考えないと無意味。
DSMは電圧方向は最初から捨てている。その方が製造上のメリットがあり、尚且つ帯域内での歪も減らせるので。両者の誤差の赤の波形が意味する所は大きい。少し想像力を働かせると、何故にデジタルフィルターのタップ数が理想フィルターとしては全く無力かの答がある。
オーバーサンプリングしないならば、横方向の解像度は6kHzを48kHzサンプリングすると、8しかない。縦は65536あったとしても、これは65536x8の解像度で、緑のような滑らかな曲線が書けるかという問題で、勿論無理。DSMは前提としてオーバーサンプリングするので、この場合は32x512の解像度で緑を描けという話になる。これはほぼ描けるので、つまりはタップ次第。オーバーサンプリング無しのPCMでは原理的に不可能。タップは無関係。
後は一次の積分器でも-66dBの歪なので、積分器の次数を上げて五次ぐらいまで増やせば、帯域内の歪は64倍のオーバーサンプリングでも、-140dBぐらいになる。これは入力に24ビットを想定すると、もう上がり。デジタルの領域での歪はないと言える数字。現実の世界では些かの制約が出るけれど、-120dBぐらいの歪は特に難しくない。これはPCMでは絶対に不可能な数字。
単純な一次のDSMを5ビットぐらいで量子化し、その誤差を視覚化するとその中身はPCMよりもずっと元の入力信号に近く、本質的な意味合いが分かる。1ビットに拘ってしまうと、尚且つ歴史的経緯に沿った回路で解析しようとすると、もうお手上げ。物理的な意味合いがまるで分らない。DSMとは基本的にデジタルのNFB回路にしか過ぎないけれど、次数を上げた実用的な回路から元の意味合いを辿るのは難しい。
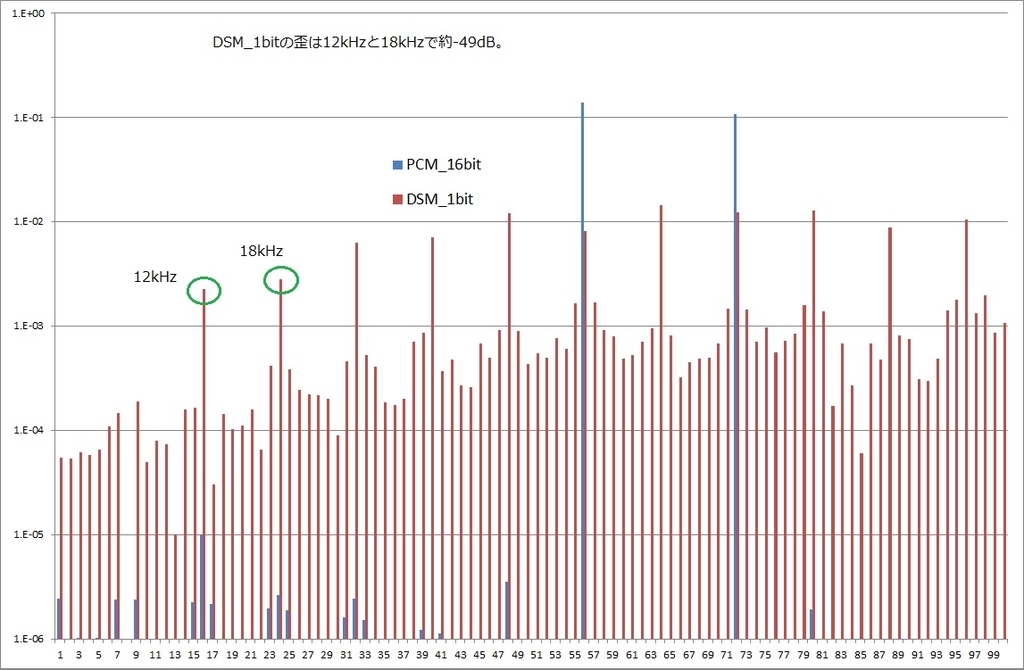
最後に参考までに1ビット。こうなってしまうので、これでは元も子もなし。頼りになるのは数式だけで直感はきかない。理学的にはアリとしても、工学的にはなし。これが使い物になるとは到底思えないけれど、意外と帯域内での歪は小さくて、 -49dB。DSMと1ビットを結びつけるべきではない。初めの1手を間違えているので、もうにっちもさっちも行かなくなる。敗着は初手にあり。これをやってしまうと、もうDSMは数式の闇の彼方に消えて行くのみ。

1ビットの場合は、多ビットの比較上1と-1で二値化。1ビットでは、二次までこのシミュレーションが可能。三次以上は必ず不安定になるので無理。その理由は意外と単純。1ビットDSMのDSDに関しては、信号を疎と密で表すと説明されることがある。嘘ではないけれど、実用的にそれはあり得ないので、そういうものは実験室以外には存在しない。
確かに上の図で、信号が最大値や最小値に近い所では出力にほとんど変化がなくて、疎になっている。二次でもだいたいこうなる。しかし3次以上では不安定。3次以上とは別の言い方をするならば、ノイズシェービングで歪をより高い周波数に持っていくという意味。そうすると一次の時のように、出力がずっと同じ状態にとどまる事は出来ない。高次のノイズシェービングとは、常に変化する密の状態でないと成り立たない。高い周波数とは、常に変化している状態。
疎は無くなって密ばかりになる。だから高い周波数に歪成分を動かせる。3次以上のDSMには密しかない。それが変調度の制約になる。1ビットの高次DSMに、50%を超える変調度はない。密を維持するために出力は常に変化している。最大値を出したい時も、1、1、1、1というような並びはなくて、1、1、-1、1のように4つのうち一つは-1を混ぜる必要がある。密のゴリ押し。
結果として、最大値は(1+1+1+1)/4=1ではなくて、(1+1-1+1)/4=0.5にしかならない。最小値も-0.5で、出せる最大振幅は2ではなくて1。その制約下で入力が絶対値で0.5以上のレベルになると、もう股裂き。忠ならんと欲すれば考ならず。腸捻転でもがいた挙句、発振するしかなくなる。帰還の係数の問題でなく、原理的に変調度は50%まで。
1ビットの3次以上が不安定になりやすいというのは嘘で、50%を超える変調度は原理的に不可能。入力のレベルを50%以下に制限しないと、高次の1ビットは機能しない。制限すれば問題なく動作する。自分で試さないと、この問題の本質は分からない。そのためか1ビットの変調度の制約に関する話は、ほとんど見かけない。5ビットぐらいあると、勿論この問題はほとんどなくなる。
現実論としては、量子化ビット数はあまり歪に関係しないので、5次であれば1ビットも変調度に気を付ければデジタル領域では実用になる。アナログにまで変換するのであればまずは無理。市販のDACチップはモノリシックで、内部にアナログ回路が入っているから実用になる。それと同じ性能を、外付けのハイブリッドで出すのは無理。
1ビットにDACの精度は不要なので、ロジックICをDACとして使うことも可能。これを更に発展させて、アナログのFIRフィルターと組み合わせると、そこそこは行く。でも色々な問題があって、数字としては90dBぐらいのSNが限界でCDには届かない。実用的には問題がないので、これは結構人気があるのも事実。
多ビット型のDSMであれば、110dBぐらいのSNは可能。これはほとんど市販のDACチップと同じ数字。FPGAと高速のRF用DACで実現可能。この組み合わせであれば、1ビットでも同じSNを確保できる。この場合は、敢えて1ビットにする理由もなくはないので。
this is abstract in english.
https://www.diyaudio.com/forums/digital-line-level/313100-physical-meaning-dsm.html